Molecular biology
Field biology
Recording and analysing data
Molecular biology
With advancing technology, scientists no longer have to rely on capturing animals or gathering data manually in the field. Bioinformatics enables the analysis of a whole genome from a computer. Once the initial DNA sequencing has taken place, a lot of research can be conducted just from that data. For example, the DNA, mRNA or amino acid sequence between two individuals or species can be compared.
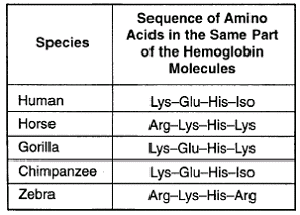
From this short sequence of amino acids in the haemoglobin of these different species we can infer several things. Let’s do humans and chimps first! How many differences are there? Lys, Glu, His, Iso and… Lys, Glu, His, Iso. Right. Absolutely no difference. Humans and gorillas have one difference, zebras and horses have one difference and zebras and humans have 3 differences!
We can infer a lot of different information from this table, and it’s just a very small sequence in just one protein looking at just five different species. The potential of investigating diversity with molecular biology tools is astounding.

DNA can be studied similarly, and a lot of creativity can be employed to come up with ways to twist and turn heaps of genetic data in such a way that interesting information can be pulled out. In this example, it’s a fairly straightforward, run of the mill comparison between the DNA sequence itself of a mouse gene versus a fly gene.
We can see that the sequence itself is 76.66% identical, while the protein product resulting from the exons only, is actually identical in its entirety at 100% between the two sequences (highlighted in green).
Field biology
Where do you even begin to count the number of organisms in a field, for example? How can quantitative data be obtained for a rocky shore? It’s not feasible to assess every single individual plant, count all the crabs you can possibly find, or estimate the abundance of all types of grass along a shingle ridge. Even if that was possible, the data would still not apply to the make up of a population, for example, at different times.
The answer is to obtain a sample. If a sample of crabs on a shore was to be taken, where would you look? In the spot where you can already see 3 of them, or in the spot where there are none? Well, in order for the sample to be representative, you must not involve yourself, as the experimenter, in the process of deciding the sample locations…
