Investigating Variation
Introduction
Types of variation in species
Intraspecific variation
Interspecific variation
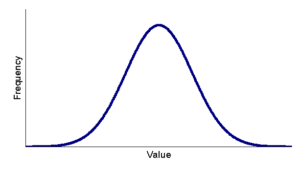
Continuous variation Normal distribution curve
Standard deviation
Variation between members of the same species is called intraspecific variation. Members of different species are easily distinguishable as very different (interspecific variation), but variation is a key concept within the same species too. So if you were to collect samples of clovers in order to analyse their height, how would you go about making sure you don’t happen to pick up all the tall ones or all the short ones? Before you’ve even analysed them, how would you know what the average height would be?
Chance plays an important role in sampling. Chance cannot be eliminated, but the probability of variation being due to chance can be decreased by collecting a large sample, and random sampling. In this case, the height of clovers would be considered continuous variation, as opposed to discontinuous. Continuous means that the clovers can have any height between certain values e.g. 2.1cm, 2.2cm or 2.25. Could one clover have a height of 2.24cm? Yes, that’s perfectly possible.
An example of discontinuous variation is the number of toes. It’s either 10, or more rarely a couple more or a couple less. So it could be 8, 10 or 12. Could someone have 12.35 toes? No.
Back to the clovers. You’ve got the data, and if you were to plot it, then what you’d get is a normal distribution curve. This means that most clovers will have about the same height, with a few deviating from the mean occurs is called the standard deviation. This shows the spread of data around the mean.