Planning
Controls
Sampling
Implementing
Analysis
Evaluation
Planning
Variables
Variables are factors present in an experiment. Often, they are the factors that we are primarily interested in e.g. testing a food variable against an age variable. Due to the nature of experiments taking place in the actual world, many confounding variables can present themselves, more or less clearly, in experiments. Confounding variables are those variables which can overlap so that it cannot be obvious whether a result is due to one variable or another. For example, in looking at people’s diets which contain both fat and sugar, these components are confounding variables of each other in a study that wants to only look at the effect of fat or sugar.
In order to tease away confounding variables from each other, a technique called randomised block design is used to categorise data into groups, and then carry out the experiment independently in each. For example, participants can be split by weight, diet, sex, height, etc. so that any findings can be said to not be due to any of these pre-split factors.
Variables vary by the type of data they can produce. Discrete variables give rise to individual data points that cannot be connected e.g. colours, whole numbers of things, blood groups. Continuous variables give rise to data that is possible on a spectrum of connected values e.g. height, width, solute concentration.
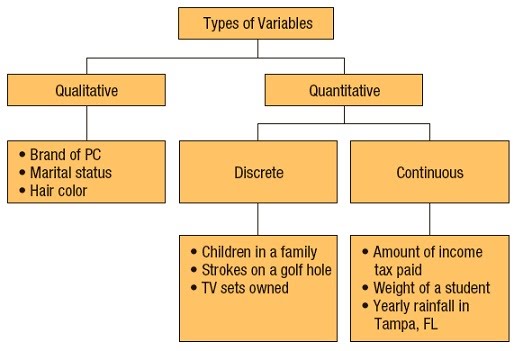
As such, the data derived can be qualitative (green, blood group B), quantitative (1.55 m, 65 nm, 50 nM NaCl) or ranked (low, moderate, high intensity).
Different data can be displayed and analysed in different ways – graphically, statistically, etc. Data can be represented in many ways e.g. bar charts, scatter plots, images, photos, tables. The type of data determines what method can be used to represent and analyse it.
Experimental design
Experimental design covers the equipment and reagents needed and whether these are safe and cost-effective enough to justify their use; what experiments will be carried out, when, in what order, how and how many times; what data will need to be recorded; what biases might arise and
how to counteract them e.g. labelling tests using codes rather than content names; how to organise experiments to fit with experimenter’s schedules or equipment booking schedules; how to collect the right amount of data from experiments to be able to use certain statistical tests afterwards i.e. some tests need a minimum of data to apply.
Things to consider during the process of developing an experimental design are the controls, dependent and…..
